
オシロスコープの測定技術
第2回:オシロスコープの立ち上がり時間と帯域
前回はオシロスコープのプローブの重要性について考えました。第2回は基本を押さえるために、波形を正しく観測するポイント、立ち上がり時間と帯域について考えてみたいと思います。たとえば、立ち上がり時間が0秒の信号をオシロスコープに入力した場合、どのような波形を得ることが出来るでしょうか?高価なオシロスコープならば、どんなに高速な信号でも正しく波形を捉えて表示してくれるのでしょうか?ここでは、オシロスコープの限界をできるだけ簡単な式で、理論的に確認し、オシロスコープやプローブが持つ帯域についても理解を深めてみましょう。
1.オシロスコープの立ち上がり時間と帯域
a. RC Low-Pass回路
デジタルオシロスコープにとって急峻な信号が入力された場合、いかにその立ち上がりを再現できるか、その立ち上がり時間をきちんと捉えることができるかが重要になりますが、現実的には遅延要因はありそれは1次のRC Low-Pass 回路 と同等の応答になります。(図1、図2)
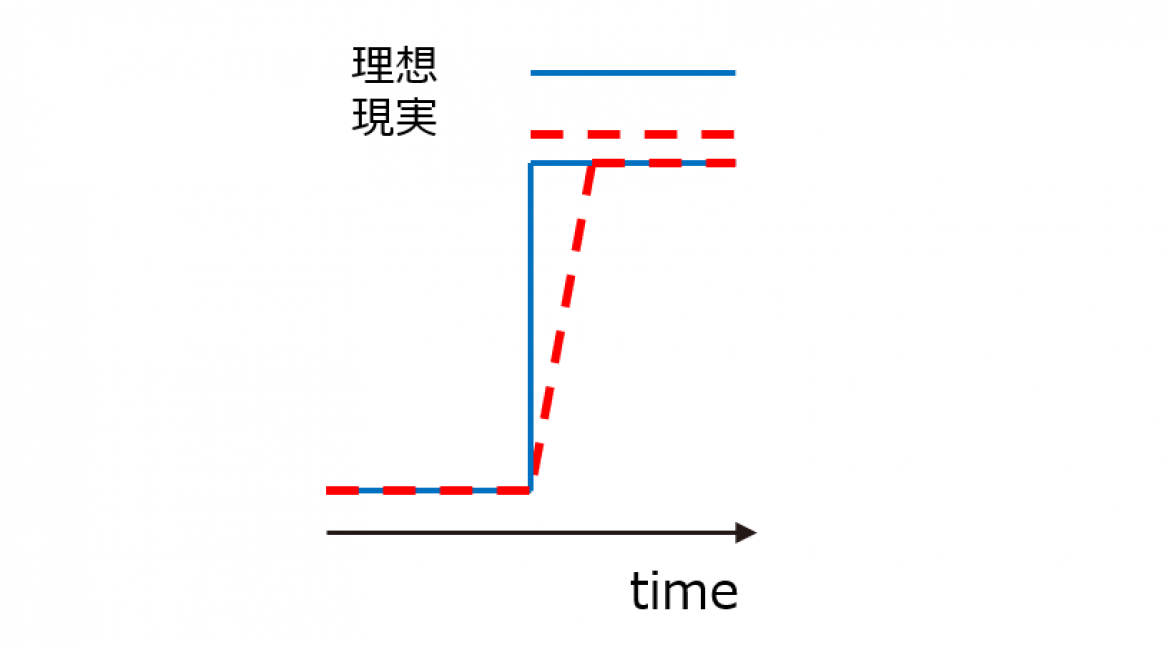
図1
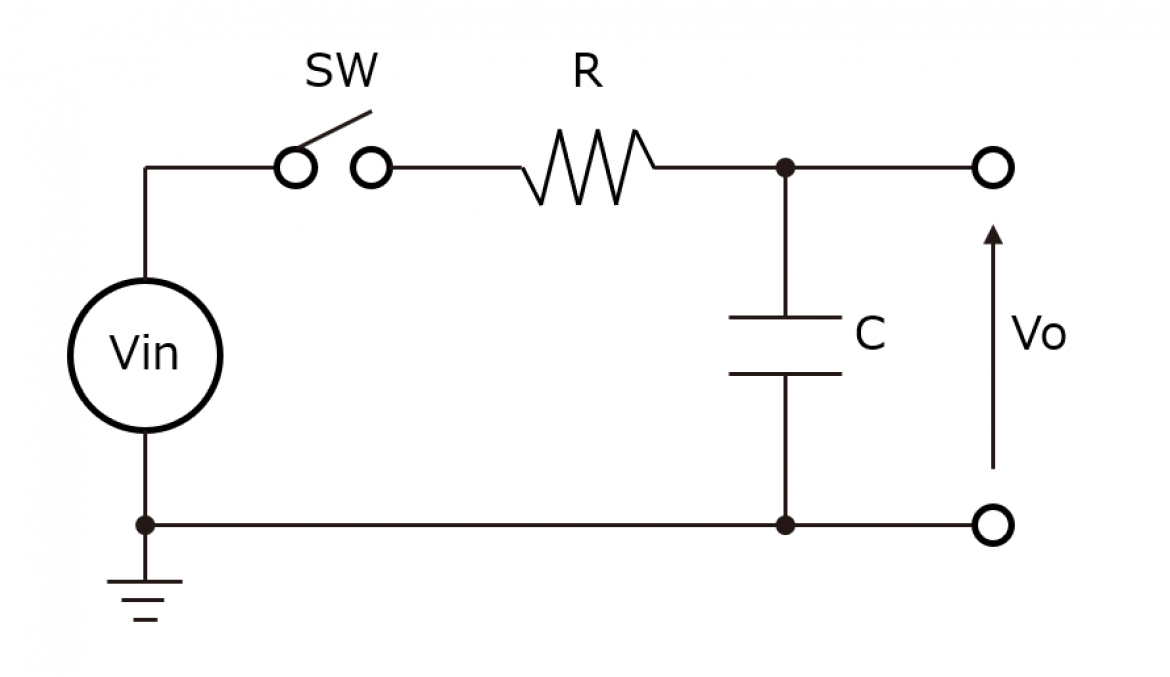
図2
そのステップ応答は、
$$Vo = Vin( 1 - e^{-t/RC }) … 1) $$
と表すことができます。
さて、図2 は、10:1のパッシブプローブ(~10MHz程度)の回路モデルの例です。
なお、各メーカーにより数値は異なりますので、製品仕様を確認してください。立ち上がり時間は、立ち上がり波形の 10%~90%(高速信号の場合は20%~80%)と定義されるので
$$10\%Vin = Vin( 1 - e^{-t10/RC} )$$より$$t10 = -RC・In0.9$$
$$90\%Vin = Vin( 1 - e^{-t90/RC} )$$より$$t90 = -RC・In0.1$$
よって、立ち上がり時間は、
$$t90-t10 = 2.197・RC … 2)$$
と計算できます。
ここで、電力利得が1/2になるときの周波数をfcとすると、RC Low-Pass回路においては、
$$RC=1⁄(2πfc) … 3)$$
の関係式が成り立ちます。(参考:電力利得が1/2になるときの周波数(fc))
2)・3)よりRCを削除すると
$$t90-t10=0.35⁄fc … 4)$$
ただし、高速のオシロスコープの場合、単純なRC Low-Pass回路で表現することは出来ず、0.35は、0.43@1GHz程度で計算すると比較的計算が合います。
参考)電力利得が1/2になるときの周波数(fc)
RC Low-Pass回路 図3 において、
$$Vo/Vin = {{1} \over {1+jωCR}}$$
絶対値をとると
$$|Vo/Vin|={{1} \over \sqrt {1+(ωcR)^2 }}$$
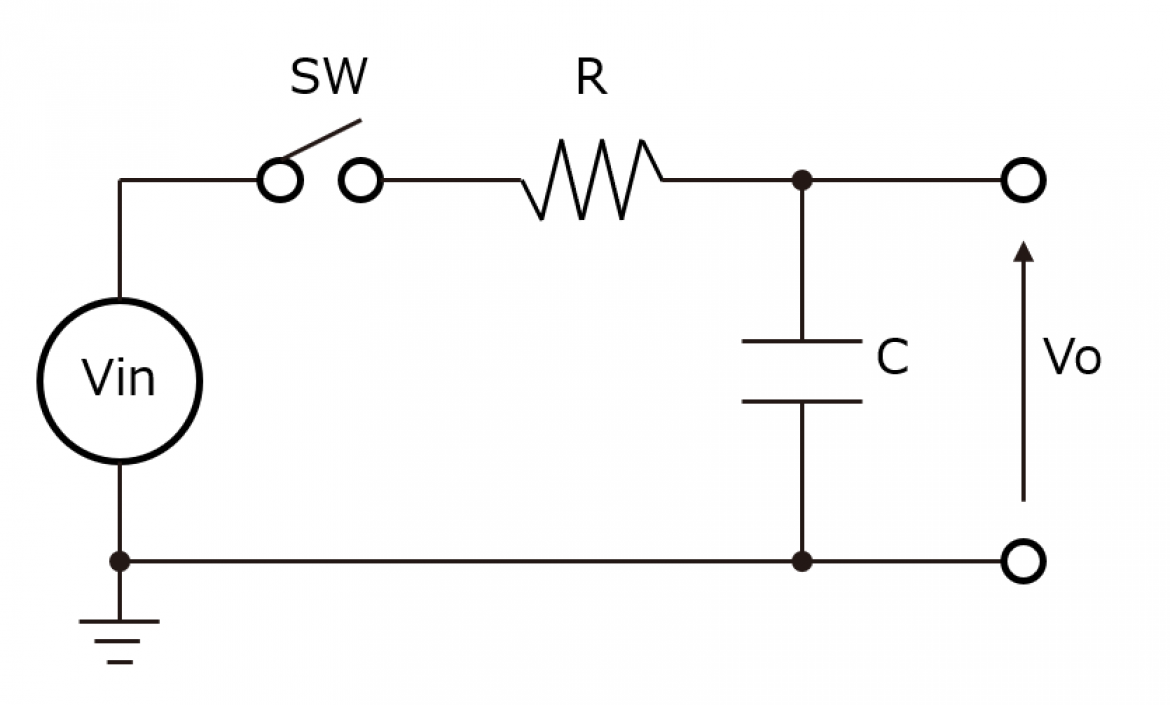
図3
ここで、電力利得
$$|Pout/Pin|=1⁄2$$になるときの周波数をfcとすると、その電圧利得は
$$|Vo/Vin|=1⁄ \sqrt {2}$$なので
$$2πfc・CR=1$$従って
$$RC=1⁄(2πfc)$$
の関係式が成り立ちます。また、このとき電力利得は、
$$10⋅log(1⁄2)=-3dB$$
になります。
b. 波形観測(オシロスコープが表示する時間:tm)
オシロスコープの立ち上がり時間 (tsys)
$$tsys= 0.35/fc … 4)$$と表すことが出来ました。
ここで、電力利得が1/2になるときの周波数fcですが、これは帯域幅を表します。
つまり、帯域 100MHz のオシロスコープ系(オシロスコープならびにプローブを含めた)を使った場合、オシロスコープ系自体の立ち上がり時間 (tsys) は、0.35/100MHz = 3.5ns となります。
ガウシアンフィルタを想定し、時定数が異なる2個のガウシアンフィルタを直列につなぐと、各フィルタの時定数の二乗和の平方根になるので、
$$観測時間(tm)=\sqrt{tr^2+tsys^2} ※ tr:実信号の立ち上がり時間$$と表すことができます。
測定される時間には、オシロスコープ観測システムが持つ立ち上がり時間 (tsys) が常に加算されることになります。評価において、この値を誤差と捉えられるかどうか、十分に検討をすることが大切です。
c. 帯域幅と正確に測れる範囲
帯域幅は、出力電力がピーク値(電力利得)の1/2になる周波数と定義します。
その式は、
$$10log {{Pout} \over Pin} = 20log {{Vout} \over Vin} = -3dB = 20log0.707$$で表されます。
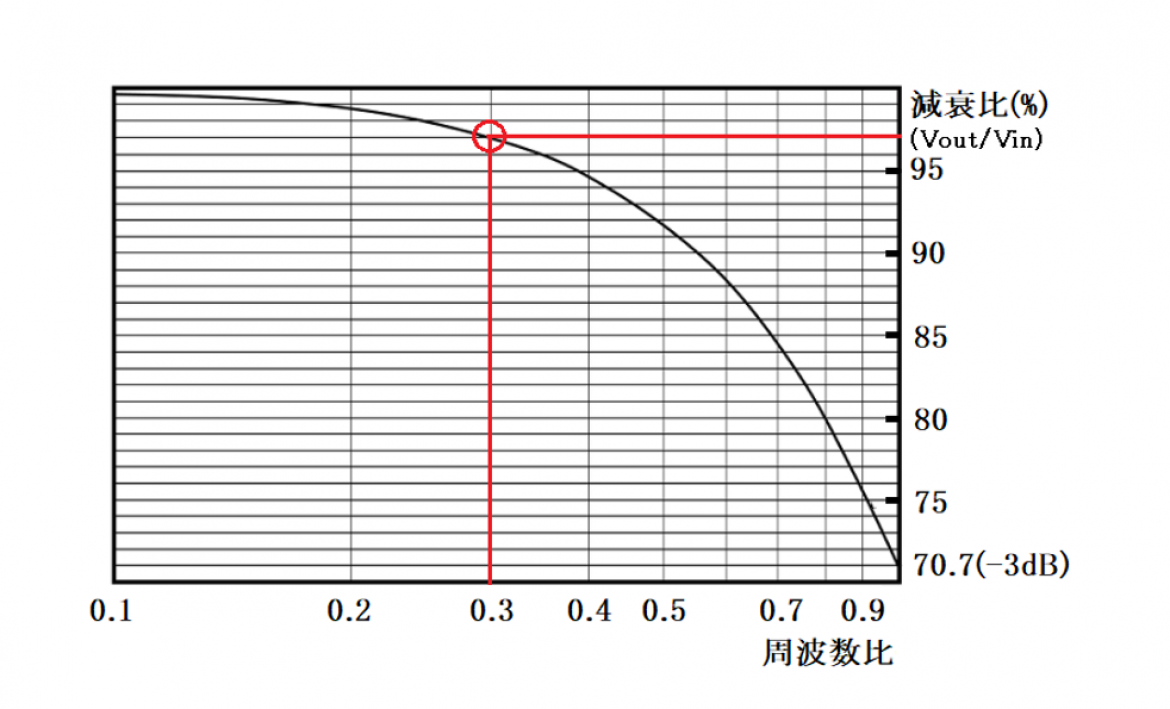
図4
この式は、-3dB帯域幅近くで測定を行うと、Vout/Vin=0.7 程度となり、Voutの振幅は、70% 程度として捉えられてしまうことを示しています。つまり、30% もの誤差が発生してしまうことを意味します。
図4は、オシロスコープの帯域比と減衰比(Vout/Vin)を示しています。ここで、帯域 500MHz のオシロスコープを仮定した場合、周波数比 0.3、すなわち 150MHz における減衰比は、97% です。
つまり、帯域 500MHz のオシロスコープで 3% 程度の誤差を許容した場合、測定できる周波数は 150MHz 以下 ということになります。周波数帯域が十分でないと、高周波成分であるエッジ部分は消え、振幅が低下し、詳細な信号観測ができなくなります。
一般的に
『 オシロスコープの帯域幅(Hz)≫観測信号成分の最高周波数×5 』
という、5倍ルールがあります。
この時、誤差は2%以下(図の周波数比0.2に相当)になります。
通常のアプリケーションにおいては、この考え方で十分で、200MHz の信号を 2% の誤差で扱う場合、1GHz の帯域幅のオシロスコープで測定することが望ましいということになります。
2. デジタルオシロスコープの選び方
皆様の実験室にあるデジタルオシロスコープは、誰かが何らかの製品の特性を測定するために選択をしたことと思います。さて、どのようにして選択をしたのでしょう。
- オシロスコープの帯域幅(Hz)≫ 観測信号成分の最高周波数 × 5
- 8bitマイコンを扱うならば350MHz程度は欲しい。
- チャネル数
- 同時測定ポイントとして、アナログ信号観測には4chは欲しいところです。
- 数10chをカバーしたロジックアナライザ機能を持つものもあります。
- サンプリングレート ≫ オシロスコープの帯域幅(Hz) × 4
- 特別なことがなければ、各chが1GS/s、最大2GS/sで、一般的なアナログ信号の観測ならば十分です。
- レートが高いほど高額になります。どれくらいの分解能が必要となるのかを考慮して決める必要があります。
- メモリ長 ≻ サンプリングレート × 表示時間
- タイムベースを考慮して仕様を確認します。自動調整がされてしまうケースもあります。
- メモリ長が長い解析は、演算時間が長くなることがあり、表示に時間がかかることがあります。また、この時、次の波形を取り込むことができない状態にあります。
- 波形取り込みレートが高いものを考慮します。
- 上記を考慮されれば、表示機能やトリガ機能等々は十分な物が自然に選択されることと思います。ただし、波形解析機能については、オプションを含めて仕様を確認してください。
- プローブの帯域とオシロの帯域は、低い方で測定限界が決まります。
- 1GHz オシロスコープと 500MHz パッシブプローブで測定を行う場合、帯域幅は 500MHz になります。
- その他、アクティブプローブ等は、実信号への影響を少なくすることができます。
まとめ
2回に渡り、オシロスコープ、プローブによる評価において、注意点、また波形が持つ誤差、さらにオシロスコープの測定限界について考えてきました。実際、まだまだオシロスコープについてはきちんと理解をしておくべき特性・現象は沢山あります。評価において事前に観測波形の期待値を確認し、適切な機器を選択し、十分なマージンを持って波形の観測をお願いいたします。〈完〉
PDF資料請求
バックナンバー
Global Design Notes について
Global Design Notes は、エンジニアのための役立つ技術情報を掲載した WEB 連載です。
- 発行元:グローバル電子株式会社
- 公開メディア: https://www.gec-tokyo.co.jp/design-notes

